Расчет индуктивно связанных электрических цепей

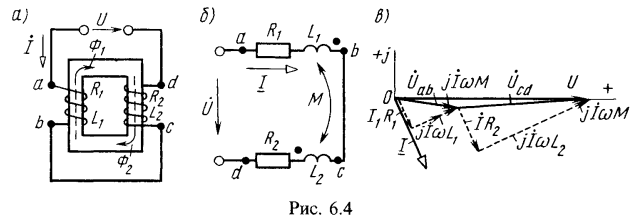
Расчет индуктивно связанных электрических цепей 1. Определить эквивалентное комплексное сопротивление цепи (рис. 6.4, а), ток и напряжения между точками а и b, с и d, если известны

Решение:
Проследив по рис. 6.4,а прохождение тока по виткам обеих катушек, видим, что в каждой из них
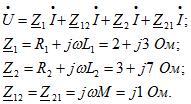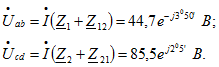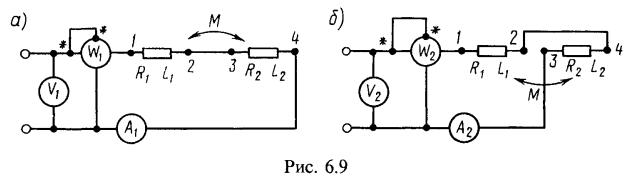
потоки самоиндукции и взаимной индукции действуют согласно. Таким образом, катушки включены согласно. Заданную цепь можно представить схемой, показанной на рис. 6.4,б. Составим для нее уравнение второго закона Кирхгофа: Эквивалентное комплексное сопротивление цепи Искомый комплексный ток Комплексные напряжения между точками а и b, с и d: На рис. 6.4, в изображена векторная диаграмма. По вещественной оси отложен вектор напряжения, от него в сторону отставания на направлен вектор тока, затем отложены векторы падения напряжения в каждой из катушек.2. Для определения взаимной индуктивности двух катушек их соединили последовательно и подключили к источнику, были измерены напряжение, ток и мощность в двух случаях: а) зажим 2 первой катушки соединен с зажимом 3 второй катушки (рис. 6.9, а), б) зажим 2 первой катушки соединен с зажимом 4 второй катушки (рис. 6.9, б). Показания приборов при первом опыте: ; при втором . Чему равна взаимная индуктивность катушек, если частота переменного тока f=50 Гц? Выяснить, в какой из двух схем катушки соединены согласно.

Решение:
По данным первого опыта найдем полное сопротивление схемы , ее резистивное и реактивное сопротивления :

Аналогично из данных второю опыта: Равенство полученных значений резистивного сопротивления свидетельствует об отсутствии ошибок измерения. Реактивное же сопротивление во втором опыте оказалось больше, чем в первом . Это указывает на то, что вторая схема соответствует согласному включению, а первая — встречному.
Искомую взаимную индуктивность найдем из уравнений: Вычитая одно уравнение из другого, получим

3. Даны две параллельно соединенные катушки (рис. 6.11,а), параметры которых и сопротивление взаимной индукции . К цепи подведено напряжение U=150 В. Найти токи и построить векторную диаграмму. Определить показание каждого ваттметра и мощности тепловых потерь в каждой из ветвей.Решение:
Из рис. 6.11,а видно, что катушки соединены согласно, так как каждую из них магнитные потоки само-и взаимной индукции пронизывают в одном и том же направлении. На рис. 6.11,б начерчена схема заданной цепи. Введем обозначения:

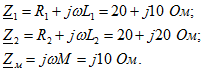
По законам Кирхгофа: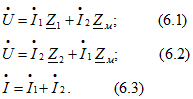
Решив совместно уравнения (6.1) и (6.2) и приняв , получим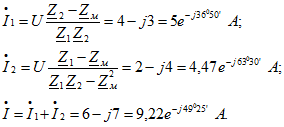

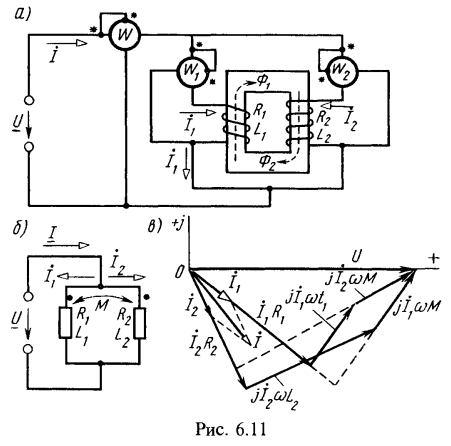
На рис. 6.11,в по уравнениям (6.1) —(6.3) построена векторная диаграмма. По вещественной оси отложен вектор U. На основе расчетов построены векторы . Затем на основании уравнения (6.1) построены векторы ; их сумма дает вектор U. Аналогично построены векторы по уравнению (6.2). Определяем показания каждого из ваттметров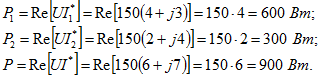 Тепловые потери в первой и второй ветвях а их сумма равна мощности Р, поступающей во всю рассматриваемую цепь (900 Вт).
Активная мощность , потребляемая первой ветвью от источника энергии, частично расходуется на тепловые потери в этой ветви , а остальная часть (600-500=100 Вт) поступает в магнитное поле, откуда вследствие взаимной индукции передается во вторую катушку. Это видно из следующего.
Напряжение взаимной индукции на первой катушке

а мощность, передаваемая полем из первой катушки во вторую,

Аналогично,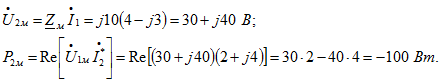

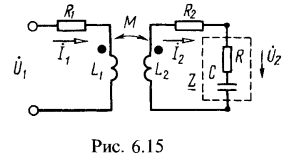
4. К первичной обмотке трансформатора без стального сердечника подведено напряжение (рис. 6.15). Определить напряжение на нагрузочном сопротивлении при
Решение:
Система уравнений второго закона Кирхгофа для этого случая

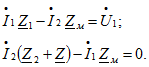Решая эти два уравнения, получим 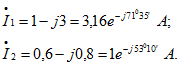Напряжение на сопротивлении

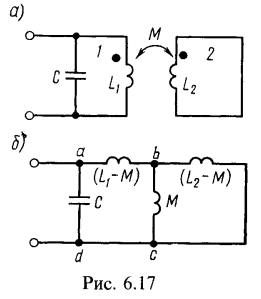
5. Колебательный контур 1 без потерь индуктивно связан с короткозамкнутой цепью 2 (рис. 6.17, а). Чему равна резонансная частота, если ?Решение:
Резонанс токов наступит, когда реактивная проводимость равна нулю. Вычислим ее, начиная с определения эквивалентного комплексного сопротивления двух параллельных ветвей, подключенных к точкам b и с:

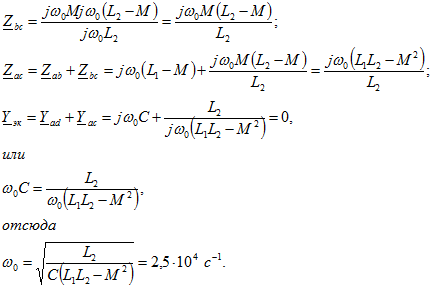
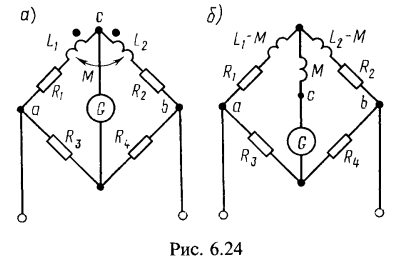
6. В схеме цепи (рис. 6.24, а) определить , при которых мост уравновешен. Дано: . Найти входное сопротивление цепи, если

Решение:
Воспользовавшись развязкой индуктивных связей, преобразуем исходную схему (рис. 6.24, а) в эквивалентную, не содержащую взаимных индуктивностей (рис. 6.24,б); при этом следует обратить внимание на появление новой узловой точки. Для последней схемы записываем условие равновесия моста Приравняем соответственно вещественные и мнимые составляющие:
.
Решая эти уравнения, найдем Определим входное сопротивление цепи

Смотри полное содержание по представленным решенным задачам.