Трансформаторы (страница 1)

Электромагнитные процессы в трансформаторе при холостом ходе

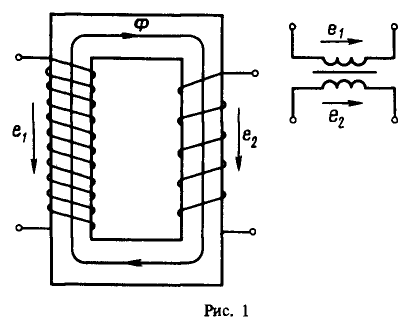
1. Установив, что задача связана с описанием электромагнитных процессов в трансформаторе при холостом ходе, дадим схемную интерпретацию данной задачи. Изобразим электромагнитную схему однофазного трансформатора и его условное графическое развернутое обозначение (рис. 1). Для произвольно выбранного направления силовых линий главного магнитного поля укажем направления ЭДС взаимной индукции в обмотках.

Числовые значения величин: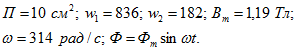
Определить: Решение:
Подберем нужные формулы из теоретического раздела параграфа и подставим в них числовые значения заданных величин, предварительно выразив их в СИ.
Действующее значение ЭДС первичной обмотки

Магнитный поток в магнитопроводе выразим через магнитную индукцию и активное сечение стали магнитопровода: С учетом (2) Аналогично рассчитывается действующее значение ЭДС вторичной обмотки: Амплитуды ЭДС в обмотках: Мгновенные значения ЭДС при синусоидально изменяющемся магнитном потоке: Пользуясь приложением 2, проверим размерность вычисляемых величин: Ответ:

Электромагнитные процессы в трансформаторе при нагрузке 2. Задача относится к разделу "Электромагнитные процессы в трансформаторе при нагрузке" и, как следует из условия, требует графического решения с помощью векторной диаграммы.
Числовые значения величин: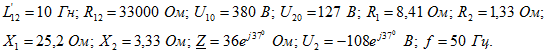

Определить: Решение:
Приступая к решению задачи, проведем небольшой предварительный анализ. Векторная диаграмма трансформатора является графической интерпретацией системы уравнений трансформатора. Запишем эту систему: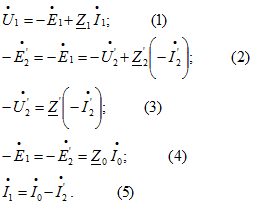 Сравнив систему (1)-(5) с исходными данными, легко заметить, что условие задачи позволяет непосредственно определить комплексные сопротивления первичной и вторичной обмотки: . Входящее в (4) полное сопротивление первичной обмотки при холостом ходе можно найти по исходным данным с учетом дополнительных соотношений: Для решения системы необходимо величины вторичной обмотки привести к первичной, для чего надо знать значение коэффициента трансформации, которое в свою очередь можно определить по заданным величинам . Если к искомым по условию задачи величинам добавить неизвестную величину , то получим систему пяти уравнений с пятью неизвестными. Решим эту систему графически с помощью векторной диаграммы.
По (6) определим индуктивное сопротивление (или сопротивление взаимной индукции) и величину активного сопротивления .
Определим коэффициент трансформации и приведенные вторичные величины: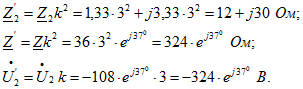 Перейдем к определению искомых величин. Приведенный вторичный ток трансформатора а его реальная величина (действующее значение)
Чтобы определить остальные величины, построим векторную диаграмму. Учитывая активно-индуктивный характер нагрузки, начало координат временной комплексной функции поместим в левом нижнем углу листа формата 200x170 мм, направляя действительную положительную ось по горизонтали (рис. 2).

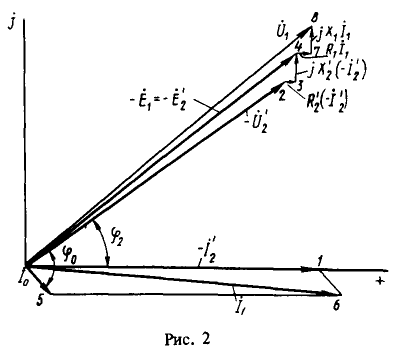
Выбрав масштаб тока 1 см = 0,1 А, отложим на действительной оси обратный комплекс вторичного приведенного тока .
Выбрав масштаб напряжения 1 см = 30 В, отложим обратный комплекс приведенного вторичного напряжения .
Определим значения активной и реактивной составляющих падения напряжения на вторичной обмотке: Из конечной точки вектора отложим в масштабе напряжения параллельно току вектор , по величине равный 12 В : 30 В/см = 0,4 см, и перпендикулярно — вектор , равный 30 В : 30 В/см = 1 см. Соединив конец этого вектора с началом координат, получим вектор ЭДС взаимной индукции , по величине равный .
Рассчитаем действующее значение тока холостого хода и фазового угла: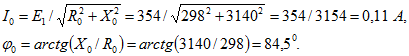 Под углом к направлению вектора отложим на диаграмме отрезок .
В соответствии с (5) векторная сумма токов определяет первичный ток трансформатора . Из построений видно, что .
Для определения первичного напряжения рассчитаем значения активной и реактивной составляющей падения напряжения на первичной обмотке и с конца вектора отложим векторы (рис. 6.2), по величине равные .
В результате получим вектор первичного напряжения , действующее значение которого .
Для удобства последовательность графических операций на рис. 6.2 показана цифрами 1-8.
Ответ:

Несимметричная нагрузка трехфазных трансформаторов

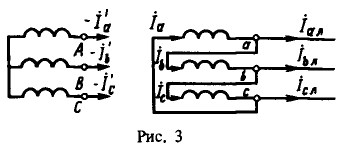
3. Задача относится к теме "Несимметричная нагрузка трехфазных трансформаторов" и связана с определением искажения симметрии первичных фазных и вторичных напряжений при заданной несимметричной нагрузке. Условие задачи полезно проиллюстрировать схематичным изображением трехфазного трансформатора, включенного по схеме и нагруженного несимметричными токами (рис. 3).

Числовые значения величин: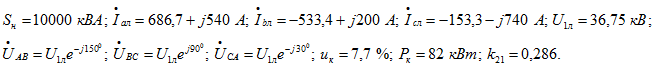

Определить: Решение:

Анализируя условие задачи, отметим, что при соединении обмоток по схеме вторичные и соответственно первичные токи не содержат токов нулевой последовательности. В этом случае первичные и вторичные токи уравновешивают друг друга, поток и ЭДС нулевой последовательности равны нулю, а фазные первичные напряжения при симметричных линейных напряжениях получаются симметричными и определяются положением центра тяжести треугольника линейных напряжений. Вторичные фазные напряжения отличаются от первичных на величину падения напряжения на сопротивлении короткого замыкания.
Комплексные величины линейных первичных напряжений, заданные в показательной форме, запишем в комплексной алгебраической форме:

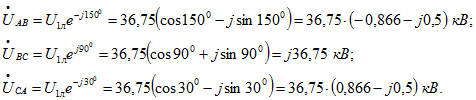При отсутствии тока (потока и ЭДС) нулевой последовательности фазные первичные напряжения: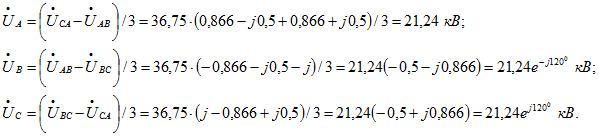
Видно, что трехфазная система первичных фазных напряжений симметрична.

Полученные соотношения можно проиллюстрировать графическими построениями векторной и топографической диаграмм (рис. 4). Размещая начало координат временной комплексной функции в центре листа, направляем действительную положительную ось по вертикали.

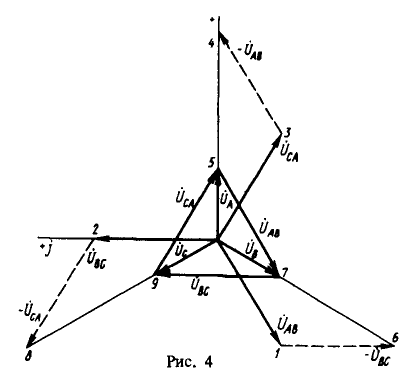
Выберем масштаб напряжения 1 см = 7 кВ и отложим векторы линейных напряжений . Прибавим к вектору вектор и возьмем третью часть полученного вектора, в результате имеем искомое фазное первичное напряжение . Аналогично строятся векторы . Соединив концы векторов, получим топографическую диаграмму - треугольник линейных напряжений. Легко убедиться, что фазные напряжения определяются "центром тяжести" треугольника.
Как уже отмечалось, вторичные напряжения трансформатора отличаются в данном случае от первичных на величину падения напряжения на сопротивлении короткого замыкания.

Определим составляющие полного сопротивления короткого замыкания, используя соотношения: . Найдем номинальный фазный первичный ток , полное сопротивление короткого замыкания его активная и реактивная составляющие: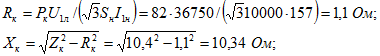 комплекс полного сопротивления короткого замыкания Чтобы определить вторичные фазные токи при заданном соединении обмотки в треугольник, воспользуемся соотношениями: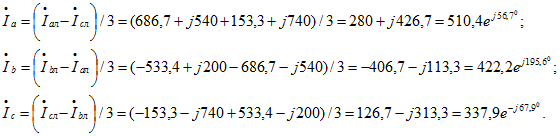
Приведенные значения вторичных фазных токов: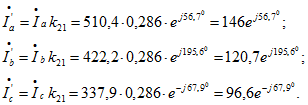 Падения напряжения на сопротивлении короткого замыкания: 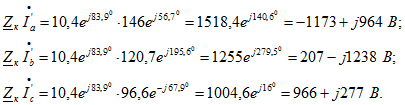Приведенные вторичные фазные напряжения: 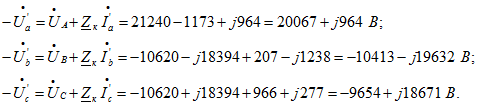Вторичные фазные напряжения: 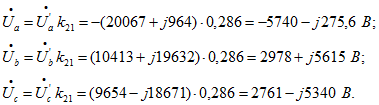При заданной схеме соединений вторичной обмотки линейные напряжения равны фазным.

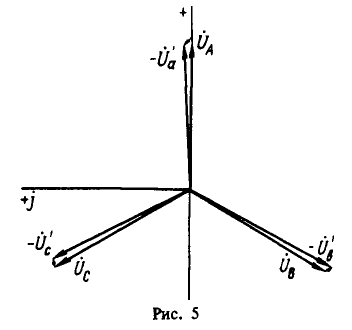
Для графической иллюстрации полученного решения построим векторную диаграмму первичных и вторичных напряжений трансформатора. Выбрав масштаб напряжения 1 см = 4 кВ и разместив начало координат временной комплексной функции в центре листа формата строим векторы первичных напряжений (рис. 5):

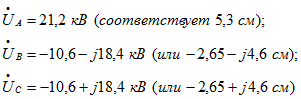и обратные векторы приведенных вторичных напряжений: 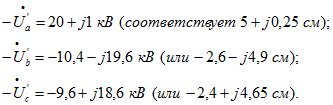Как видно из рис. 5, искажение симметрии вторичных фазных напряжений из-за симметрии токов сравнительно невелико, что обусловлено отсутствием токов нулевой последовательности.

Ответ: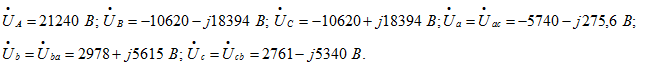

Смотри полное содержание по представленным решенным задачам.