Величины и единицы освещения

Величины и единицы освещения

ВЕЛИЧИНЫ И ЕДИНИЦЫ

Световой поток (Ф) - мощность лучистой энергии, оцениваемая по производимому ею световому" ощущению. Единица - люмен (лм) имеет размерность кандела X стерадиан.

Сила света (I или J) - отношение светового потока к телесному углу, в котором он излучается. Единица - кандела (кд). Сила Света является одной из основных величин в системе СИ.

Телесный угол (w) - часть пространства, заключенная внутри конической поверхности. Измеряется отношением площади, вырезаемой им из сферы произвольного радиуса, к квадрату последнего. Единица - стерадиан (ср).

Освещенность (E) - отношение светового потока к площади, на которую он распространяется. Единица освещенности - люкс (лк) имеет размерность люмен на квадратный метр. Освещенность поверхности не зависит от ее свойств и от направления, в котором поверхность рассматривается.

Яркость (L) - отношение силы света в данном направлении к площади проекции излучающей поверхности на плоскость, перпендикулярную данному направлению. Единице яркости - кандела на квадратный метр (кд/м2) - собственного наименования не присвоено. При прочих заданных условиях яркость определяет зрительное ощущение, которое, однако, ей не пропорционально.

Светимость (М) - отношение светового потока к площади излучающей его поверхности. Единице - люмен на квадратный метр (лм/м2) - собственного наименования не присвоено.

Приводятся определения тех же величин в математической форме:

(1-1)

Те же выражения в недифференциальном виде дают средние значения величин в пределах определенных площадей или углов.

До внедрения системы СИ применялись символы: F вместо Ф, В вместо L, R вместо М. Единица силы света именовалась свечой, единица яркости - нитом.

Изменения величин единиц не произошло, т. е. кандела = свече, кандела на квадратный метр = ниту.

СВЕТОРАСПРЕДЕЛЕНИЕ ИЗЛУЧАТЕЛЕЙ

В общем случае поток излучателя произвольно распределяется в пространстве и светораспределение характеризуется фотометрическим телом: геометрическим местом концов векторов, выходящих из светового центра излучателя, длина которых пропорциональна силе света в соответствующем направлении.

Сечение фотометрического тела меридиональной плоскостью дает меридиональную кривую силы света, графически изображающую зависимость , где a - угол между направлением силы света и вертикалью.

Круглосимметричиое светораспределение (фотометрическое тело имеет ось симметрии) исчерпывающе характеризуется одной меридиональной кривой, которая обычно и называется кривой силы света.

Во многих случаях (большинство светильников с трубчатыми лампами) фотометрическое тело имеет две плоскости симметрии, соответственно чему различаются поперечная и продольная меридиональные (это слово в практике опускается) кривые силы света.

В наиболее общем случае (отсутствие оси или плоскостей симметрии) светораспределение характеризуется многими меридиональными кривыми силы света, диаграммами изокандел и т. д.

Кривые силы света чаще всего строятся и наиболее наглядны в полярных координатах. Для прожекторов они даются в прямоугольных координатах, что также предпочтительно для расчетов -повышенной точности.

В некоторых теоретических случаях светораспределение может быть выражено аналитически, а многие реально имеющие место кривые силы света достаточно близки к описываемым простыми уравнениями, что имеет большое значение при расчетах и анализах.

Часто оказывается пригодной формула

(1-2)

При m = 0 она соответствует равномерному светораспределению диффузного шара, при m = 1 - косинусному светораспределению диффузного диска (такому диску эквивалентна любая вогнутая диффузная поверхность с плоским выходным отверстием).

Для диффузного полушара с несветящей горизонтальной экваториальной плоскостью

(1-3)

эта же формула дает поперечную кривую силы света диффузного полуцилиндра.

Употребительна также формула

(1-4)

хотя практически с достаточной точностью ее можно заменить выражением

(1-4а)

Наконец, для диффузного вертикального цилиндра с несветящими торцами

(1-5)

СВЕТОВОЙ ПОТОК И СИЛА СВЕТА

Элементарный телесный угол, образованный вращением угла da вокруг вертикальной оси, с которой он образует угол a

(1-6)

Конечный телесный угол круговой зоны, ограниченной направлениями и

(1-7)

световой же поток, заключенный в этой зоне,

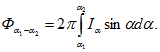(1-8)

При светораспределении, заданном аналитически, интеграл берется:

для равномерного источника (шар) ;

для диффузного диска ;

для диффузного цилиндра ;

для люминесцентной лампы из-за неполной диффузности излучения ;

для диффузного полушара ;

для случая применимости выражения (1-2)

;

это же выражение может быть использовано для определения показателя m в нижней полусфере:

(1-9а)

Для круглосимметричных светильников, светораспределение которых задано кривой или таблицей, поток определяется умножением зональных телесных углов на силу света в направлении середины каждой из зон и суммированием произведений, так что

(1-10)

Значения зональных телесных углов для десятиградусных зон приведены в табл. 1-1.

Определение потока светильников с трубчатыми лампами, имеющих две плоскости симметрии, производится в следующем порядке:

значения силы света в направлениях 5, 15, 25, ... , 85° продольной плоскости умножаются на значения телесного угла w:

Таблица 1-1 Зональные телесные углы

Интервал меридионального угла, град		Телесный угол, ср
Нижняя полусфера	Верхняя полусфера
0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 80-90	170-180 160-170 150-160 140-150 130-140 120-130 110-120 100-110 90-100	0,095 0,283 0,463 0,628 0,774 0,897 0,992 1,058 1,091
		6,28=2p

a, град	5	15	25	35	45
w, ср	0,0303	0,0294	0,0276	0,0249	0,0215
a, град	55	65	75	85
w, ср	0,0174	0,0129	0,0079	0,0027

Делением удвоенной суммы произведений на осевую силу света находится вспомогательный коэффициент (эту величину, иногда называемую коэффициентом формы).

Находится сумма значений сил света в направлениях 5, 15, 25, ..., 85° поперечной плоскости , после чего искомый поток

(1-11)

Для каждой из полусфер вычисления производятся отдельно.

При косинусном светораспределении в продольной плоскости .

Таблица 1-2 Тригонометрические функции

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44	0,000 0,0175 0,035 0,052 0,070 0,087 0,104 0,122 0,139 0,156 0,174 0,191 0,208 0,225 0,242 0,259 0,276 0,292 0,309 0,326 0,342 0,358 0,375 0,391 0,407 0,423 0,438 0,454 0,469 0,485 0,500 0,515 0,530 0,545 0,559 0,574 0,588 0,602 0,616 0,629 0,643 0,656 0,669 0,682 0,695	0,000 0,0175 0,035 0,052 0,070 0,088 0,105 0,123 0,140 0,158 0,176 0,194 0,213 0,213 0,249 0,268 0,287 0,306 0,325 0,344 0,364 0,384 0,404 0,424 0,445 0,466 0,488 0,510 0,532 0,554 0,577 0,601 0,625 0,649 0,674 0,700 0,726 0,754 0,781 0,810 0,839 0,869 0,900 0,932 0,966	1,000 0,999 0,998 0,996 0,993 0,989 0,984 0,978 0,971 0,964 0,955 0,946 0,936 0,925 0,913 0,901 0,882 0,874 0,860 0,845 0,830 0,814 0,797 0,780 0,762 0,744 0,726 0,707 0,688 0,669 0,649 0,630 0,610 0,590 0,570 0,550 0,530 0,509 0,489 0,469 0,449 0,430 0,410 0,391 0,372	45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89	0,707 0,719 0,731 0,743 0,755 0,766 0,777 0,788 0,799 0,809 0,819 0,829 0,839 0,848 0,857 0,866 0,875 0,883 0,891 0,899 0,906 0,914 0,920 0,927 0,934 0,940 0,946 0,951 0,956 0,961 0,966 0,970 0,974 0,978 0,982 0,985 0,988 0,990 0,992 0,994 0,996 0,998 0,999 0,999 1,000	1,000 1,036 1,072 1,111 1,157 1,199 1,235 1,280 1,327 1,376 1,428 1,483 1,540 1,600 1,664 1,732 1,804 1,881 1,963 2,050 2,145 2,246 2,356 2,475 2,605 2,747 2,904 3,078 3,271 3,487 3,732 4,011 4,331 4,705 5,14 5,67 6,31 7,12 8,14 9,51 11,43 14,3 19,1 28,6 57,3	0,353 0,335 0,317 0,299 0,282 0,266 0,249 0,233 0,218 0,203 0,189 0,175 0,161 0,149 0,136 0,125 0,114 0,103 0,094 0,084 0,075 0,067 0,0596 0,0525 0,0460 0,0399 0,0345 0,0294 0,0249 0,0209 0,0173 0,0141 0,0113 0,0090 0,0069 0,0052 0,0038 0,0027 0,0018 0,0011 0,00066 0,00034 0,00014 0,000042 -

ОСВЕЩЕННОСТЬ И СИЛА СВЕТА

В общем случае освещенность точки

(1-12)

где Е - освещенность, лк; I - сила света по направлению к точке, кд; a - угол между нормалью к поверхности, которой принадлежит точка, и лучом; r - расстояние от источника до точки, м.

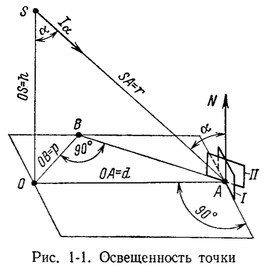
Для точки А (рис. 1-1), если она принадлежит горизонтальной плоскости, выражению (1-12) могут быть приданы, в частности, следующие формы:

Для вычисления освещенности приведена сокращенная таблица тригонометрических функций (табл. 1-2).

При неизменном h с возрастанием d обычно Е монотонно убывает. Характер убывания определяется формой кривой .

Если с увеличением a происходит возрастание , то в пределах определенных значений d можно получить постоянную или даже возрастающую с увеличением d освещенность.

При неизменном d кривая E =f(h) во всех реальных случаях имеет максимум, определяющий наивыгоднейшую высоту, которая при косинусном светораспределении равна d, при равномерном светораспределении .

Освещенность точек негоризонтальных поверхностей часто определяется умножением горизонтальной освещенности на коэффициент y.

Коэффициент y равен отношению кратчайшего расстояния источника от данной освещаемой поверхности ("высоты" его над последней) к его высоте над проведенной через данную точку горизонтальной поверхностью.

Для вертикальной плоскости y= tga, если считать точку А (рис. 1-1) лежащей в плоскости I (перпендикулярной OA), и y=p:h, если А лежит в плоскости II (общий случай).